Consider the Ellipse

In the course of chart-svg development, I’ve considered the ellipse. Quite a bit. It’s a weekender project run amok trampling on best laid plans, but life is art and I code in Haskell for art sake as much as commerce. Here’s what I saw.

Consider an angle

numhask contains a type class, Direction, which interfaces between Cartesian or spatial position and polar¹ co-ordinates, busting this information into direction and magnitude.

The best way to illustrate the Direction class is is via the Point instance in numhask-space²:

instance (TrigField a) => Direction (Point a) a where
  angle (Point x y) = atan2 y x
  ray x = Point (cos x) (sin x)

Nothing new here, except for shepherding these into a class. In base, these are available for the Complex type and are called phase and cis, a naming convention whose exact provenance is unknown to me, though I do admit to having gone through a cis phase. In linear, these are rendered as angle and unangle in typical kmettian brutalism.

Checking in with wiki, an angle, is formed by two rays.

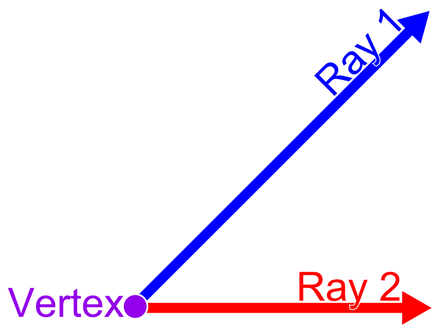
This specification of Direction locks in a frame of reference where the ray 2 of the wiki diagram refers to Point one zero (aka along the positive x-axis). The decision as to whether positive y means up (sane people) or down (SVG) then spills over to angle specification, so that a positive angle means clockwise in SVG but is anti-clockwise in grade-school³ textbooks.

Consider a circle.

Topologically, an ellipse is a circle. The unit circle is a circumference, a continuous set of points in a two dimensional frame with magnitude one.

Armed with ray we can approximate a unit circle as a list of points:

-- xs is a hundred Doubles forming a grid over [0, 2 * pi]
-- representing radians
xs = grid OuterPos (Range 0 (2 * pi)) 100 :: [Double]
unitCircle = ray <$> xs

and here’s a picture:

Consider the ellipse

In SVG land, an ellipse is then a circle that is:

• scaled by a Point (ie scaled across the x and y axis)
• rotated by an angle
• translated by a Point

For example, an ellipse with a major radius of 2, a minor radius of 1, rotated by pi/4 from the x-axis, and centered on Point 1 1 looks like:

rotate a b = norm b .* ray (a + angle b)
(Point 1 1 +) . rotate (pi/4) . ((Point 2 1) *) . ray <$> xs

Position, position, position

The SVG standards choose to define an ellipse segment in terms of the (x,y) co-ordinates of the segment ends - sometimes called endpoint-based in the standards. This contrasts with sane engineering (taking advantage of angle maths, say) and the standards acknowledge this potential, and define conversion between angle and position pov’s:

In contrast, cleaning up the code tapped out above and adding some naming arrives at a competitive standard to this:

ellipse centroid radii major theta =
  rotate major (radii * ray theta) + centroid

Much neater.

The factory must grow, but nothing prepares you for the cthulhuian emergence that is then B.2.4:

Meanwhile …

the same computation expressed in Haskell …

theta_ centroid radii major pos =
  angle . (/radii) . rotate (-major) . (- centroid) $ pos

To find the angle, the ellipse transformations each have reversals that you apply to position (who would have thunk it). No trig bleeding out all over the spec polluting the essence of the computation.

Take another look at rotate:

rotate a b = norm b .* ray (a + angle b)

I see a heavy-hitting fusion recipe for turning trig calcs into addition, easily understood and able to be recreated in most languages.

The code, as it stands, has a good chance of actually doing a sin and cos calc exactly once (linear types might cement this guarantee in) whatever the complexity of it’s context. The simplicity noted by mathematicians working on ellipses using polar co-ordinates directly translates into blindingly fast code, and this looks like the blueprint.

But that’s not all! atan infinity bugs are confined to ray (/radii will also be problematic). norm has the square root aka “magnitude must be positive” bugs well located. No corner cases, no if buts or maybes.

No x or y subscripts in plain sight, at all. We can extend to 3D either cylindrically or spherically within this class without any api change. No matrix notation messing with our diverse notions of what they mean. No flag variables.

Let’s make Haskell the lingua franca of the standards world.